Design Your Own MABR

Have you always wanted an MABR for your Wastewater Treatment Plant but feel overwhelmed by where to start?

• What do you need?

• What will it look like?

• How much membrane is required?

• How much air is required?

Well let's start at the beginning, and like other aeration technologies the first thing that must be calculated is how much oxygen is required for the biological treatment process? Pollution in wastewater is either particulate (solids) or dissolved. While biological processes can treat both, for ease of calculation, and because biological processes take a lot longer to break down solid components than settling or filtration, we will only consider the dissolved components in this calculation.

Oxygen will be required for the breakdown of Carbon Oxygen Demand (COD)  and Ammonia:

• 1kg of O2 for every kg of COD
• 4.6kg of O2 for every kg of Ammonia as N (N-NH3)

Oxygen Demand

For a typical municipal wastewater post primary treatment plant the concentrations are:

• Dissolved or Soluble COD:      300mg/l
• Ammonia as Nitrogen:    50mg/l

Multiplying these concentrations by the flowrate gives the total oxygen demand required kgO2 per day.  In the following example we will use a daily flowrate of 1000m3/day.

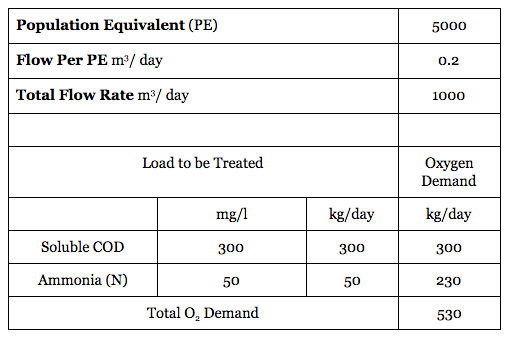
Table 1: Typical Inlet Wastewater Concentrations for 5,000 Population Equivalent

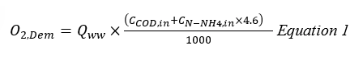
Membrane Requirements

Once the Oxygen requirement is known, the next question is how much gas permeable membrane is required to supply this O2? Taking an average Oxygen Transfer Rate (OTR) of 10gO2 /m2 of membrane per day gives a membrane requirement of:

Table 2: Calculation of Membrane Surface Area Required for Oxygen Delivery

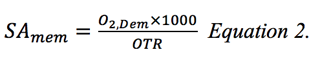
Air Requirement and Energy

The oxygen must be provided to the system and to do this air is supplied to the lumen of the hollow fibres membranes. Assuming an Oxygen Transfer Efficiency (OTE) of 50% and an oxygen concentration in the air of 21%, the air requirement is 150 Nm3/h at a pressure of 200mBar. The air supply pressure is independent of the water depth in the tank and as the air does not leave the membrane, pressure is required only to overcome the pressure loss due to airflow in the hollow fibre membranes.

The energy required to supply this air can be calculated using the Equation 4 which is taken from Metcalf and Eddy (2002), for the energy requirement for a blower, in this case using a blower efficiency of 0.65, give a power requirement of 1.25kW.

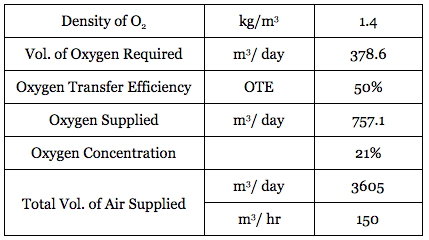
Table 3: Flow Rate of Air required

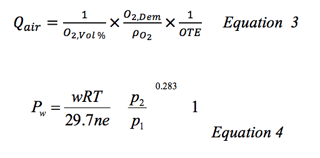
What Else is Needed?

1 . Tank

A tank of some sort is required to hold the liquid to be treated. This tank can be an existing tank e.g storm water tank, clarification tank or activated sludge tank.  The volume of the tank will depend on the packing density of the membranes. A packing density of 400-500m2/m3 is recommended.

The MABR tank can be operated in one of two modes:

• A completely mixed system where the detached biofilm and the solids are kept suspended in the liquid. These solids can then be separated from the liquid in a subsequent solids liquid separation process e.g. Settler, Dissolved Air Flotation (DAF) or Filter press

• Alternatively settling of the solids can take place directly in the tank with the MABR modules. If this is required then a settled sludge extractions system is required from the bottom of the tank. This could be a mechanical system or use the hydraulic head above the settled sludge to force it into a series of sludge extraction pipes.

The removed or separated sludge can then be further thickened or processed to increase the Solids Concentrations.

2. Mixing

Because there are no bubbles for aeration, an alternative source of mixing is required. Mixing is crucial in an MABR to ensure that the biofilm which is attached to the membrane gets in contact with the wastewater. General principles state that the mixing time for a Continuous Stirred Tank Reactor should be 10% to 20% the residence time of the reactor. Therefore the shorter the residence time the shorter the mixing time, and the more energy that is required for mixing.

Mixing also becomes more crucial at lower concentrations, as at low concentrations the rate of reaction is directly related to the concentration, and if a large stagnant layer of water develops over the surface of the biofilm due to poor or non-uniform mixing it will significantly reduce the rate of reaction and not make effective use of the biofilm. Additionally poor mixing may lead to short circuiting in the reactor. Oxymem has developed a number of clever ways of mixing an MABR, utilising the momentum of the flow as well as low energy air lift systems reusing the exhaust gas from the hollow fibre membrane.

3. Biofilm Control

While the first stage of an MABR processes is transferring Oxygen across the membrane, the next step is the consumption by the Biofilm of both the Oxygen and the pollutants. Therefore it is important to not only make sure there is enough biomass but also that the biomass is not too thick. If the biomass becomes too thick then the rate of diffusion of Oxygen and pollutants through the biofilm becomes the rate limiting step. Therefore periodically the biofilm should be scoured to remove excess biofilm and to maintain its optimal thickness.  An OxyMem MABR has an air-scour grid in the base, and scouring with coarse air bubbles takes only a few minutes, with a frequency dependant on the growth rate of the biofilm

4. Screening

Finally, good screening is important for all wastewater treatment plants. Debris such as branches, wires or ropes can get tangled with the membranes and potentially damage the hollow fibres. Ragging or hairs are not an issue in the MABR, as no filtration is taking place these solids are not pulled towards the membranes and so do not cause any issues. But additionally they are not removed by the MABR and will become part of whatever solids are removed, post biological treatment.

Nomenclature

Summary

MABR holds out the very real possibility of having a transformative impact on the way we plan, manage and operate wastewater infrastructure.  The principal  benefits are 75% Energy saving, 50% less sludge, in a greatly reduced footprint (Up to 80% reduction). Don't you owe it to yourself and your organisation to investigate further? Please try our MABR design tool for sizing your applications....